In the end of last year, I decided to change my career from artificial intelligence and machine learning to blockchain. Decentralized technology and AI are two of major forces will change the world. The deep learning is the central topic of AI in recent years. I still remember how exciting when I watched the matches between AlphaGo and Lee Sedol. Soon later, DeepMind published another paper about AlphaGo Zero which training the network from scratch with only basic Go rules without any training data from human players. This is a beautiful result. However, in many cases, the deep learning still requires a large amount of training data, the deep network is more or less like a black box to me and the training of deep network in extremely high dimentional parameter space is kind of mixure of art and science. That’s one major reason for me to switch. But in future, the two roads will merge.

I write the blog of fraud proof to help me understand Vitalik’s paper. This is the first part, it focuses on the fraud proof where one full node prove to light node that a given block is invalid.

Fraud proof (part I)

• Background
• Merkle Tree and Sparse Merkle Tree
• Fraud proof scenario
• State transition and block redesign
• Fraud proof

Background

Light node is also called SPV (simple payment verification), for example if develop an mobile app that can run blockchain transaction, it’s impractical for the mobile to download all the blocks. Instead, the app can only download the headers for all the blocks as well as the data related to user’s transaction (merkle proof). Full node is the machine that download all the blocks including all the transactions and the accounts information.

The light node does not know the full transactions and states of blockchain and all transactions of the blockchain, it cannot verify whether a block is valid. The light node has to contact other full nodes for necessary information to verify it. If all the nodes it contacts is malicious, then it can be easily tricked by the malicious full nodes, so we always assume there is at least one honest full node the light node can connect to.

Merkle Tree and Sparse Merkle Tree

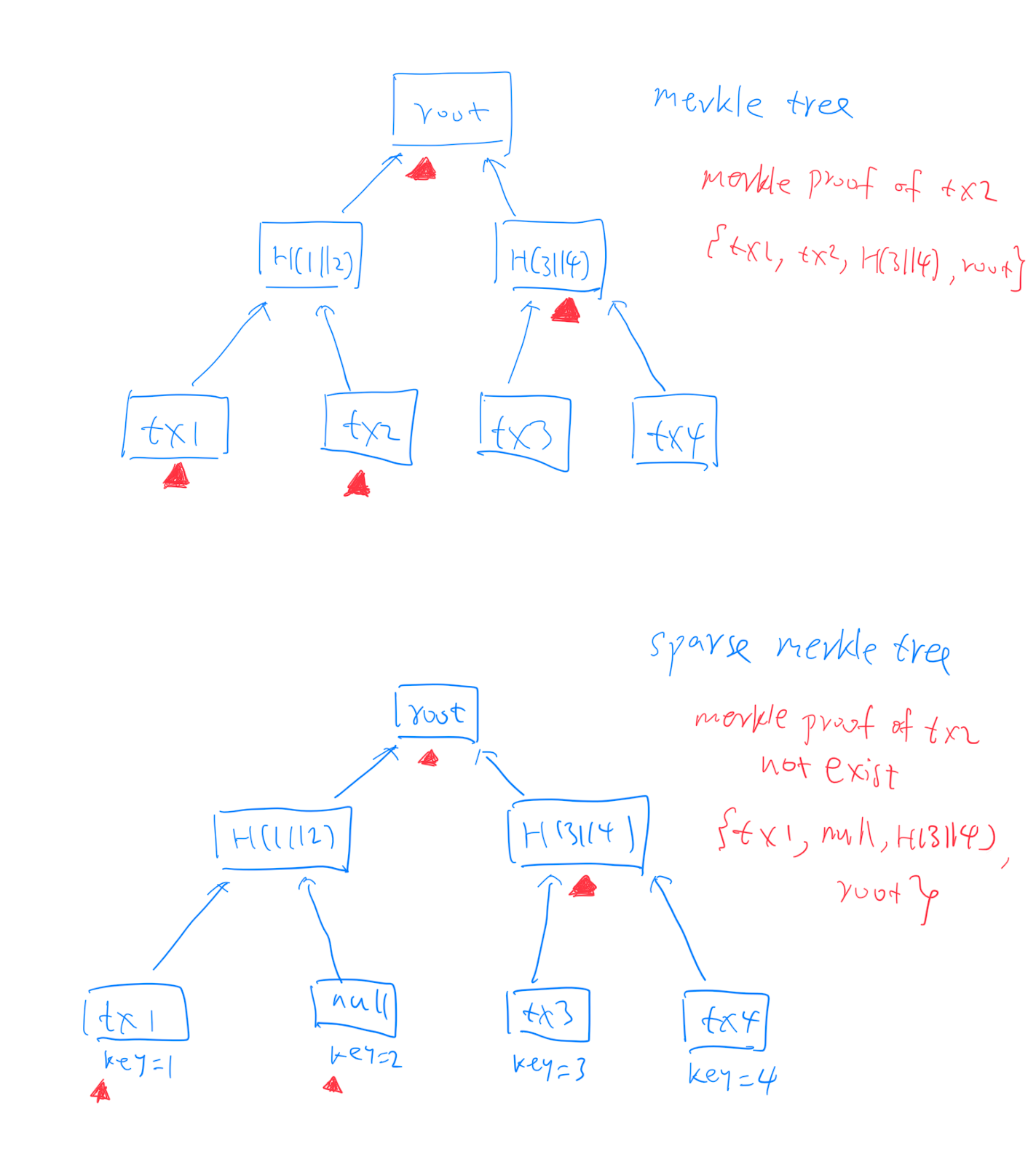
There are plenty of articles explaining the idea of merkle tree. It is efficient $O(log(n))$ way to prove a transaction is in the block. To prove one transaction is in the block, the full node can send the merkle proof to the light node. In the following image, the full node want to prove tx2 is actually in the block, he just send the corresponding merkle proof $\{tx_1, tx_2, H(3\|4), root\}$. This is $log(n)$ of the total $n$ transaction.

If $tx_2$ is not in the block, how the full node can prove it? One simple way is the light node contact other full nodes to show the proof of existence, if none of them can show the proof, it can assume $tx_2$ is not in the block because we assume there is at least one honest full node it can connect to. But this is definitely not efficient. In order for a full node prove the non-existence, here is where the sparse merkle tree come into play. The basic idea is that each of the possible transaction has its own index/location in the leaves of the merkle tree. The tree hence becomes a key-value store, where the key of a transaction is its hash, the value is just the content of the transaction. If we use SHA-256 hash to index every transaction, it means the tree has $2^{256}$ leaves! For any leaf that do not have a corresponding transaction, we define a default null value. It’s a very large tree, but it is OK because most of the leaves will just be null value and we don’t need to store them. Thus each possible transaction has its own location (i.e. the hash of the transaction will be the index of leaves in the huge tree). Suppose $H(tx_2)$ corresponds to second leaf (image below). The full node can use the correctness of $\{tx_1, null, H(3\|4), root\}$ to prove $tx_2$ is not in the tree. In practice below, we use sparse merkle tree to prove a state is valid or not, the idea is exactly the same.

Fraud proof scenario

When a miner create a new block, it begins from state of previous block and apply one transaction at a time to change the state, whenever it gets an error, the block is invalid. If there is no error after apply all transactions, then the block is valid. Following the same scenario, to prove a block is invalid, a full node just need to show that part of the trace of the state transitions are wrong. It needs address 3 more issues:

1. The pre_state and post_state exist in the blockchain history
2. The accounts that the transaction changes are valid in the pre/post states
3. The transaction transforms the pre_state into post_state correctly (consistency)

State transition and block redesign

State

At each given moment of time, the block is at some state. To describe a state, there are currently two widely used model: UTXO model and account model. UTXO model is used in bitcoin and account model is used in Ethereum. In UTXO model, at any given moment, the state is collection of all the valid UXTO. For any UTXO, we can use its hash as key and a binary true/false value to indicate its validity (invalid means either it doesn’t exist or already spent). In account model, the state is collection of all the key-value pair, where the key is the hash of account and the value is the value of tokens this account had. Here we ignore the contract account and contract data used in Ethereum for simplicity, but the principle is the same. Both two cases can be treated same as key value pair. As we discuss before, as long as the user has the sparse merkle tree header of that state, the full node can easily prove whether a given UTXO/account is in that state by using sparse merkle tree. This solve the second issue.

State transition

When a transaction happens, some of the accounts in the state are changed. From this perspective, each transaction is a state transition function. Since we use sparse merkle tree root to describe a state, the transaction also induce a transition function from pre-stateRoot to post-stateRoot. To solve the third issue, we simply apply the transaction to its pre_stateRoot and compare it with the post_stateRoot. I.e. verify StateRootTransition(preStateRoot, tx) == postStateRoot.

Block header redesign

To address the first issue, we need redesign our block header. Usually block header contains the hash of previous block (prev_hash), the merkle root of all the transactions(txRoot) and other additional information. The new fraud proof block header contains dataRoot instead of txRoot. dataRoot is the merkle tree root of the trace of transactions. In this case, the purpose of dataRoot is to prove the existence of both transactions and the states. Here I modify the data structure of fraud proof a little bit, which is less efficient but more clear to me.

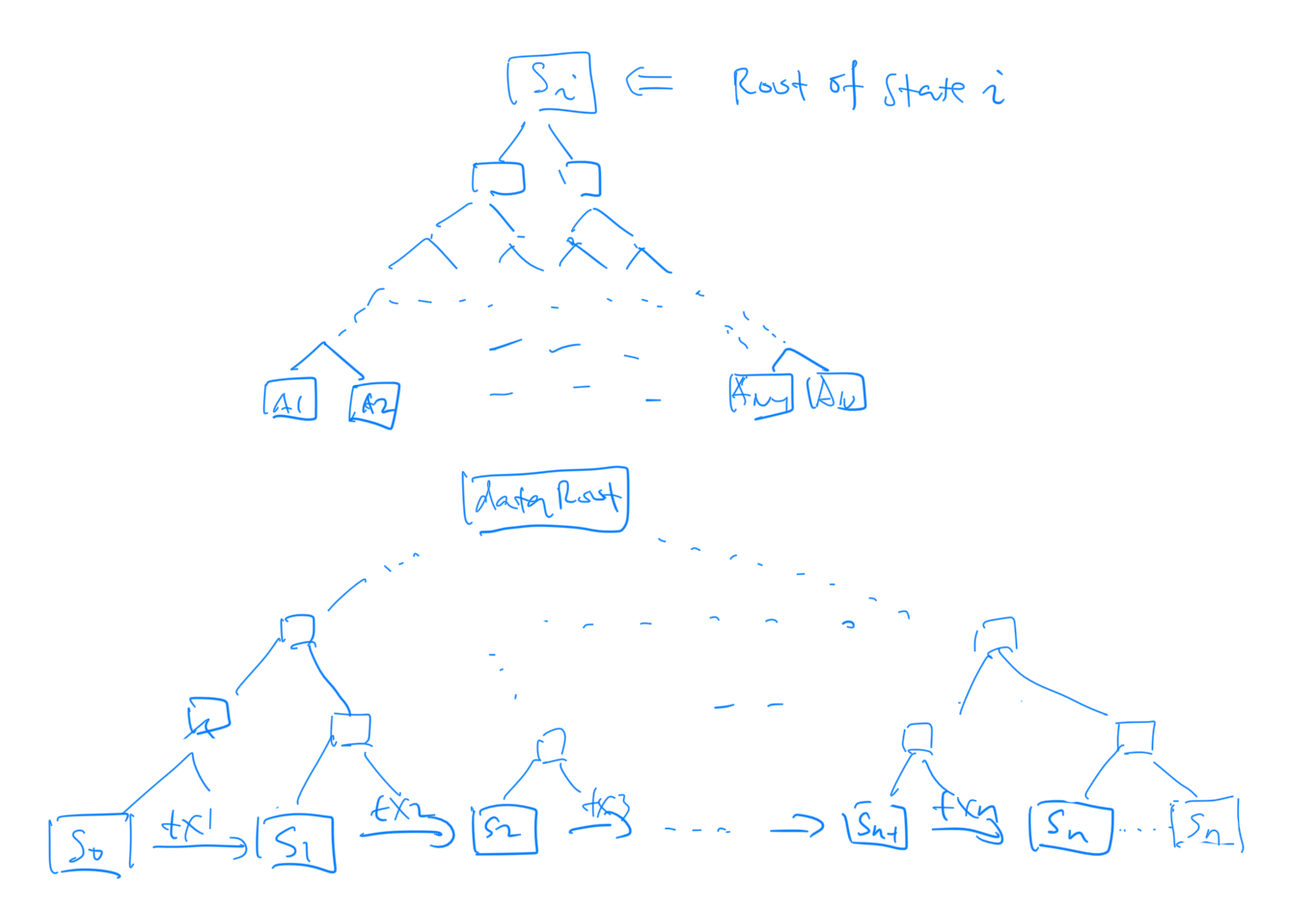
We first sort the transactions in the topological order (i.e. in the right order with no causality conflict), we include the location of transaction as part of its information. Beginning from stateRoot of previous block ($S_0$), each transaction will change the state until reach the stateRoot of the current block $S_n$ assuming there are $n$ transactions.Here $S_i$ is the sparse merkle tree root of state $i$. $tx_i$ will transform $stateRoot_{i-1}$ to $stateRoot_i$. By include the dataRoot in the header, we can easily prove whether a state or a transaction exists in the current block history. This solve the first issue.

Fraud proof

Now let’s assume that one transaction $tx_2$ is invalid. The full node provides the following information: the merkle proof that $S_1$ and $S_2$ exist (using dataRoot); the merkle proof of accounts which $tx_2$ changes are valid (using $S_1$ and $S_2$ as the tree roots); The light node can verify if $tx_2$ is valid based on all these information. In practice, we don’t have to calculate and store all the intermediate state root in the block, instead we can do it every $p$ transactions. In the paper, the authors split the whole data into equally size pieces called shares. Each share is a leaf. But the essential idea is the same as shown in above image.